Littl qonuni
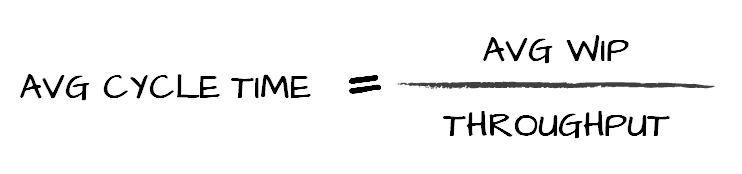
Kundalik hayotimizda biz ko’pincha navbatlarda kutishga duch kelamiz. Bu esa rejalashtirilmagan vaqt yo’qotilishiga olib keladi va ko’pchilikka yoqmaydi. Massachusets Texnologiya Institutining professori Jon D.S. Littlning quyidagi formulasi yordamida ularni nazorat qilish mumkin:
L = λW
Bu yerda: L - tizimdagi mijozlarning o’rtacha soni, λ - mijozlarning o’rtacha kelish tezligi, W - ularning tizimda bo’lishining o’rtacha davomiyligi.
Ushbu nisbat barcha tizimlar uchun universal hisoblanadi. Shifokor qabulida, bankda yoki davlat muassasasida navbatda o’tirib, kutish zalida o’rindiqlar soni nazariyaga mos kelishini tezda hisoblash mumkin. Masalan, agar yangi tashrif buyuruvchi har 3 daqiqada kelsa va navbatda 15 daqiqa kutish kerak bo’lsa, unda o’rtacha navbatda 5 kishi bo’ladi.
Formula intuitiv jihatdan sodda ko’rinishiga qaramay, u mijozlarning kelishi va kutish jarayonlari parametrlarining statistik taqsimotiga, mijozlarga xizmat ko’rsatish ketma-ketligiga (logistikada LIFO va FIFO usullari natijaga ta’sir qilmaydi) bog’liq emas. Qonun yakka xizmat ko’rsatish tuguniga ham, tarmoqqa ham amal qiladi. Butun tizimni ham, uning alohida qismlarini ham baholash mumkin. Yagona shart - tizim muvozanatda bo’lishi kerak, ya’ni ishni boshlash va tugatish jarayonida emas.
Littl qonunining qiymati uning universalligidadir - bu har qanday tizim uchun umumiy qonundir. Jarayonlarni ong osti darajasida chuqurroq tushunish uchun analogiyalarni ko’rib chiqish juda foydali. Agar ishlab chiqarish haqida gapiradigan bo’lsak, formula yordamida butun korxona, alohida tsex yoki ikki operatsiya orasida ishlab chiqarish jarayonida bo’lgan detallar sonini hisoblash mumkin. Bunda parametrlar quyidagi qiymatlarni oladi:
L - bizni qiziqtirgan uchastkada (korxonada) tayyorlanmalar soni (WIP yoki Work-in-process), λ - ularning uchastkaga kelib tushish intensivligi yoki butun korxonaning vaqt birligida ishlab chiqarilgan tayyor mahsulotlardagi unumdorligi (TH yoki throughput), W - uchastkada bo’lish vaqti yoki ishlab chiqarishning umumiy tsikli (CT yoki cycle time),
Bir nechta oddiy misollar keltiramiz:
WIP = CTxTH
Plitalarni kesish uchastka soatiga o’rtacha 600 ta detal ishlab chiqaradi. Keyingi operatsiya (qirralarni qoplash) boshlanishidan oldin har bir detal o’rtacha 20 daqiqa kutadi. Demak, ushbu operatsiyalar orasidagi detallar soni WIP=(600/60)*20=200 ni tashkil qiladi. Bu natijadan, masalan, bufer zonasi o’lchamini hisoblash uchun foydalanish mumkin. Agar qabul qilinsa-ki, bir pallet (aravachada) 50 ta detal joylashsa, to’rtta pallet joylashtirish uchun joy bo’lishi kerak.CT = WIP/TH
Biz bo’yoq kamerasidan oldin aravalarda o’rtacha 50 ta detal borligini hisobladik. Ma’lumki, jilvirlash stankidan har 2 daqiqada yana bitta detal keladi. Littl formulasiga ko’ra, CT=WIP/TH = 50/2 = 25 daqiqa - bo’yashdan oldin har bir detalning o’rtacha kutish vaqti.TH = WIP/CT
Fabrikada o’rtacha 50 ta detaldan iborat 200 ta pallet borligini bilamiz. Ishlab chiqarish tsikli 5 smenani tashkil qiladi. Unumdorlikni TH=WIP/CT=(200*50)/5= 2000 detal/smena deb hisoblash mumkin.
Littl qonuni juda oddiy vosita, lekin ba’zan soddalik yomon hazil o’ynashi mumkin. Hisob-kitoblar natijalari haqiqatga mos kelishi uchun quyidagi uchta narsani eslab qolish kerak: qonun asoslangan taxmin, formulaga qaysi dastlabki parametrlarni qo’yish mumkinligi va natijalarni sog’lom aql hamda boshqa usullar bilan solishtirib ko’rish.
Endi ushbu bandlarning har birini alohida tushuntiramiz:
Qonun tizim barqaror, muvozanat holatida bo’lgan sharoitda amal qiladi. Bu shuni anglatadiki, agar buyurtmalar soni keskin o’zgarsa va WIP hajmi tez ko’paysa, vaziyat barqarorlanmaguncha qonundan foydalanib bo’lmaydi. Bunday holatlar yangi ishlab chiqarishni ishga tushirish yoki uzoq tanaffusdan keyin ishni boshlash paytida yuzaga kelishi mumkin.
Tizimdagi uchala parametr ham - bu o’rtacha qiymatlar. Bunda o’rtachalash uzoq vaqt davomida sodir bo’lishi bilan cheklanadi. Ya’ni, formuladan foydalanishdan oldin ishlab chiqarish tizimini o’rganish, parametrlar qanchalik tez o’zgarishi (tebranishi)ni aniqlash, ularning qiymatlarini qaysi davr uchun o’rtachalash mumkinligini tushunish kerak.
Odatda, Littl qonuni ishlab chiqarishda tugallanmagan ishlab chiqarish hajmi (Work in Progress/WIP) ning tsikl vaqtiga (ishlab chiqarish zanjirining o’tkazuvchanlik qobiliyatiga) ta’sirini o’rganish uchun qo’llaniladi. Bunda unumdorlik doimiy deb qabul qilinadi. Biroq, yuqorida ko’rsatilganidek, teskari masalani ham hal qilish mumkin - unumdorlikni hisoblash va haqiqiy ishlab chiqarish ma’lumotlari bilan solishtirishdir. Masalan, ma’lum bir uchastka smenada o’rtacha 2000 ta detal chiqarishini bilasiz va agar Littl qonuni WIP va tsikl davomiyligidan kelib chiqqan holda boshqa natija bersa, bu nomuvofiqlik sabablarini izlash uchun turtki bo’lishi mumkin va bu yashirin muammolarni hal qilishning kaliti bo’lishi mumkin.
Littl qonuni ishlab chiqaruvchilarga beradigan asosiy narsa - bu ishlab chiqarish tsiklining davomiyligi ishlov berilayotgan tugallanmagan mahsulotlar miqdoriga to’g’ri proporsional ekanligini tushunishdir.
Fikrlarimizni yakunlab shuni ta’kidlash joizki, Littl qonuni - bu har qanday tizimning unumdorligini, samaradorligini va kutish vaqtini boshqarishda muhim vosita. U ishlab chiqarish, xizmat ko’rsatish, logistika va hatto kundalik hayotda qo’llanilishi mumkin. Ushbu sodda, ammo kuchli qonunni tushunish va undan foydalanish tizimlarni optimallashtirish va samaradorlikni oshirishga yordam beradi. Bunday umumiy qonuniyatlarni bilish har bir menejer va tizimli fikrlovchi uchun juda muhimdir.
